
To determine the limits of integration, we take the outermost variable and work inward. The integral will have the general form
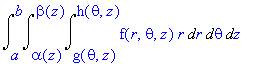
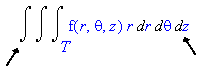
Since z is between 0 and 4, the limits of the first integral sign are 0 and 4.
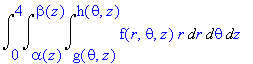
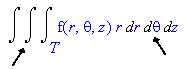
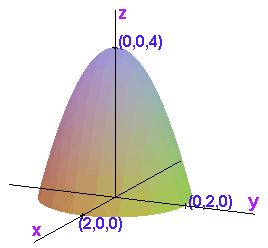
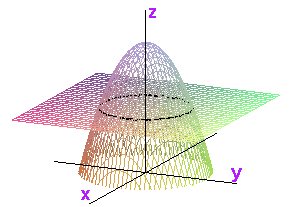
The slice formed by keeping z constant is a ball.
θ is between 0 and 2π.
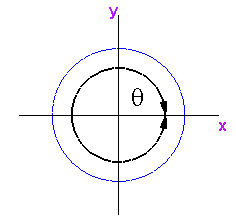
Thus the limits of the middle integral sign are 0 and 2π.
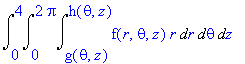
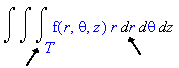
Solving for r in the equation z = 4 - r2, we get that r = sqrt(4-z).
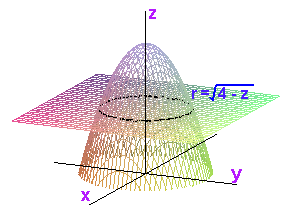
Since r is between 0 and sqrt(4-z), these are the limits of the innermost integral sign.
Thus the final integral is as follows:
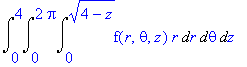
Back to Integrating Using Cylindrical Coordinates.
Back to Describing Surfaces Using Different Coordinate Systems.