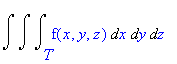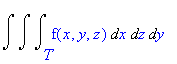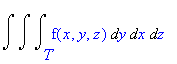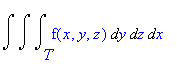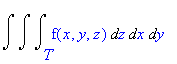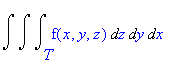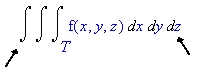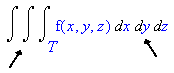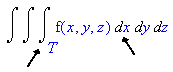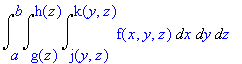Integrating in Rectangular (Cartesian) Coordinates
Recall that when using Riemann Sums to estimate an integral we divide up a solid into small pieces of dimension Δx by Δy by Δz.
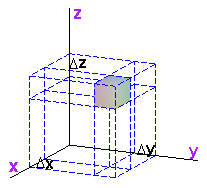
The shaded box has volume ΔxΔyΔz. Therefore, when we integrate a function f(x,y,z) over a solid T in rectangular coodinates, we use
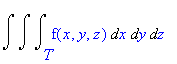
We can also change the order of integration if T is a basic solid (the boundary is a finite number of continuous surfaces--see Calculus One and Several Variables 8th Ed. Salas/Hille/Etgen pg 999.) Thus the following integrals are all equivalent:
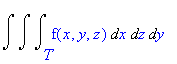
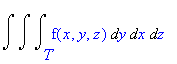
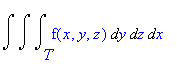
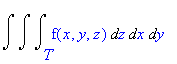
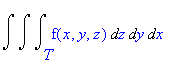
Basic Steps in Determining the Limits of Integration
To determine the limits of integration, we take the outermost variable and work inward. Sketching the graph of the solid T is extremely helpful.
Here are the basic step for integrating in the order dx dy dz. Other orders are similar.
- Determine the maximum and minimum values of the outermost variable. These will be the limits of integration on the first integral sign.
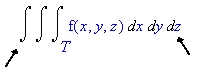
- View a slice formed by keeping the outermost variable constant. Now determine the maximum and minimum values of the middle variable within that slice in terms of the outermost variable. This will give the limits of integration for the middle integral. Note that if the maximum and minimum values depend on where the slice is taken, you will need to split the integral.
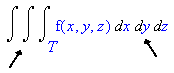
- Finally, using the same slice, determine the range of the innermost variable in terms of the other two variables. This will give the limits of integration for the inner integral. Note that if the range of the innermost variable changes within the slice, you will need to split the integral.
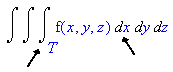
The integral will have the general form
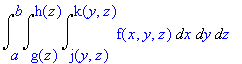
Example
We will integrate over the solid T formed by taking all nonnegative (x,y,z) under the plane 3(x-2) + 2y + 6z = 0. It is the tetrahedron with vertices (0,0,0), (2,0,0), (0,3,0), and (0,0,1).
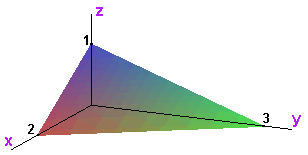
Orders of Integration for Example Solid
Back to Describing Surfaces Using Different Coordinate Systems.