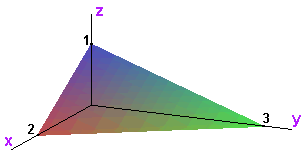
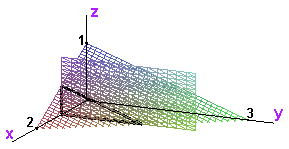
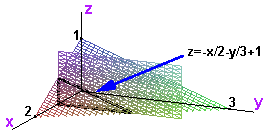
Let T be the solid formed by taking all nonnegative (x,y,z) under the plane 3(x-2) + 2y + 6z = 0. It is the tetrahedron with vertices (0,0,0), (2,0,0), (0,3,0), and (0,0,1).

To determine the limits of integration, we take the outermost variable and work inward. The integral will have the general form
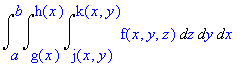
Since x is between 0 and 2, the limits of the first integral sign are 0 and 2.
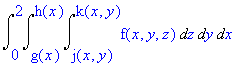
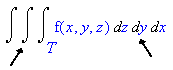
The slice formed by keeping x constant is a triangle.
The line formed where the plane 3(x-2) + 2y + 6z = 0 intersects the xy plane is y = -3x/2 + 3. This is found by letting z = 0 in the equation 3(x-2) + 2y + 6z = 0.
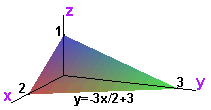
Therefore we can label the bottom vertex of the triangle formed by the slice.
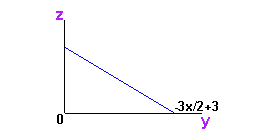
Since y is between 0 and -3x/2 + 3, the limits of the middle integral sign are 0 and -3x/2 + 3.
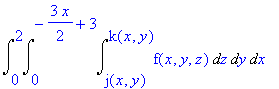
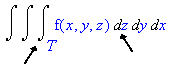
The hypotenuse of the triangle formed by taking a slice of the solid with x constant lies on the plane 3(x-2) + 2y + 6z = 0. We solve this equation for z and get z = -x/2 - y/3 + 1.
Since z is between 0 and -x/2 - y/3 + 1, these are the limits of the innermost integral sign.
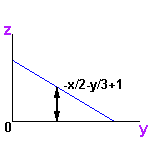
Thus the final integral is as follows:
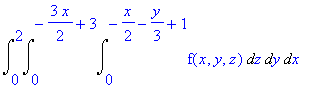
Back to Integrating Using Rectangular Coordinates.
Back to Describing Surfaces Using Different Coordinate Systems.