Setting up an Integral Over a Solid with Order of Integration dz dr dθ
Example
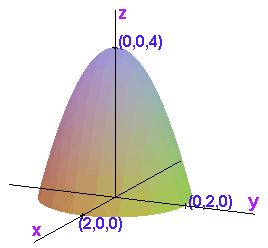
We will integrate over the solid T formed by taking all nonnegative (r,theta,z) under the paraboloid z = 4 - x2 - y2. We convert the equation of the paraboloid to cylindrical coordinates, getting z = 4 - r2.
Basic Steps with Order dz dr dθ
To determine the limits of integration, we take the outermost variable and work inward. The integral will have the general form

- Determine the maximum and minimum values of the outermost variable. These will be the limits of integration on the first integral sign.

θ is between 0 and 2π

Therefore the limits of the first integral sign are 0 and 2π.

- View a slice formed by keeping the outermost variable constant. Now determine the maximum and minimum values of the middle variable within that slice in terms of the outermost variable. This will give the limits of integration for the middle integral. Note that if the maximum and minimum values depend on where the slice is taken, you will need to split the integral.

The slice formed by keeping θ constant is shown below.

r is between 0 and 2 and doesn't depend on θ.

Thus the limits of the middle integral sign are 0 and 2.

- Finally, using the same slice, determine the range of the innermost variable in terms of the other two variables. This will give the limits of integration for the inner integral. Note that if the range of the innermost variable changes within the slice, you will need to split the integral.

We again view the slice formed by keeping θ constant.

z is between 0 and 4-r2.

The final integral is as follows:

Other Orders of Integration
Back to Integrating Using Cylindrical Coordinates.
Back to Describing Surfaces Using Different Coordinate Systems.













